viernes, 5 de diciembre de 2008
Figuras Cuadricas
Las librerías GLUT y GLU tienen funciones predefinidas para su uso con OpenGL, en lo que refiere a gráficas tridimensionales para superficies cuadráticas y superficies cúbicas, de forma sólida o alámbrica, y que tienen a la vez esta las funciones de traslación y rotación ya hechas. Además estas funciones vienen con criterios de parámetros como longitud y latitud que especificarán la cercanía de los “paños” que conformarían una de las figuras.


Photon Mapping
Desarrollado por Jensen como una alternativa a las técnicas de trazado de rayos basadas enteramente en Monte Carlo (illumination maps y ray tracing). El fin era obtener las mismas ventajas pero con un método más eficiente que no sufriera complicaciones por el ruido.
Para ello parece correcto pensar que hay que usar el mismo algoritmo basado en el trazado de rayos y además hay que procurar un algoritmo eficiente de transporte de la luz en la escena ya que tanto las luces como el observador son parte primordial de la síntesis de imágenes. También queremos utilizar técnicas de Monte Carlo vistas anteriormente pero con la certidumbre de que la componente de radiación se mantiene suave a lo largo de grandes regiones para la mayoría de los modelos. Para estas regiones parece razonable pues, almacenar y reutilizar la información extraída sobre su iluminación. Y todo ello sin dividir las superficies en trozos finitos, queremos que nuestro modelo maneje cualquier tipo de objeto.
La primera idea para solucionar el problema es pues, la de desacoplar la representación de la iluminación de la geometría. Esto nos permite tanto manejar geometría arbitraria como modelos complejos.
La segunda idea es que la iluminación en la escena puede ser almacenada como puntos en una estructura de datos global (el mapa de fotones). Muchas alternativas a los puntos fueron consideradas pero todas fallaban en una de las tres condiciones: capacidad de representar cualquier tipo de iluminación, estar desacoplado frente a la geometría y ser compacto. Por eso los puntos son la manera más flexible posible de manejar superficies de cualquier tipo de BRDF. Estos puntos además de su posición almacenarán también información sobre la dirección de incidencia de la luz y otros factores que nos facilitarán los cálculos.
El mapa de fotones puede entenderse como una caché de caminos de luces en un trazado de caminos (path tracing) direccional y podría ser utilizado ciertamente para tal método. Pero también puede usarse en un método diferente de estimación de la iluminación basada en la estimación de densidad. Esta estimación de densidad tiene la ventaja que su error es de una frecuencia mucho más baja que el que se da en los tradicionales métodos de Monte Carlo. Además el método de estimación de densidad es mucho más rápido que un trazador puramente basado en Monte Carlo. Sin embargo pagamos el precio de utilizar una estimación de densidad y por tanto un método que no nos dará siempre un rendimiento correcto, y que siempre dependerá de que para que converja más a la solución correcta se deberán almacenar y utilizar cuantos más fotones mejor.
El método del mapeado de fotones es un método de dos pasos donde los pasos son:
1. Trazado Fotónico (Photon Tracing), construir el mapa de fotones trazando fotones desde las luces y a a través de la escena.
2. Radiación estimada (Radiance Estimate), estimar la radiación producida en un punto de la escena mediante estimación de densidad.
Así el mapa de fotones será construido usando 'Trazado fotónico' donde los fotones son emitidos desde las luces y almacenados al interactuar con las superficies del modelo. Una vez construido el mapa de fotones lo utilizaremos para calcular la luz radiada.

Para ello parece correcto pensar que hay que usar el mismo algoritmo basado en el trazado de rayos y además hay que procurar un algoritmo eficiente de transporte de la luz en la escena ya que tanto las luces como el observador son parte primordial de la síntesis de imágenes. También queremos utilizar técnicas de Monte Carlo vistas anteriormente pero con la certidumbre de que la componente de radiación se mantiene suave a lo largo de grandes regiones para la mayoría de los modelos. Para estas regiones parece razonable pues, almacenar y reutilizar la información extraída sobre su iluminación. Y todo ello sin dividir las superficies en trozos finitos, queremos que nuestro modelo maneje cualquier tipo de objeto.
La primera idea para solucionar el problema es pues, la de desacoplar la representación de la iluminación de la geometría. Esto nos permite tanto manejar geometría arbitraria como modelos complejos.
La segunda idea es que la iluminación en la escena puede ser almacenada como puntos en una estructura de datos global (el mapa de fotones). Muchas alternativas a los puntos fueron consideradas pero todas fallaban en una de las tres condiciones: capacidad de representar cualquier tipo de iluminación, estar desacoplado frente a la geometría y ser compacto. Por eso los puntos son la manera más flexible posible de manejar superficies de cualquier tipo de BRDF. Estos puntos además de su posición almacenarán también información sobre la dirección de incidencia de la luz y otros factores que nos facilitarán los cálculos.
El mapa de fotones puede entenderse como una caché de caminos de luces en un trazado de caminos (path tracing) direccional y podría ser utilizado ciertamente para tal método. Pero también puede usarse en un método diferente de estimación de la iluminación basada en la estimación de densidad. Esta estimación de densidad tiene la ventaja que su error es de una frecuencia mucho más baja que el que se da en los tradicionales métodos de Monte Carlo. Además el método de estimación de densidad es mucho más rápido que un trazador puramente basado en Monte Carlo. Sin embargo pagamos el precio de utilizar una estimación de densidad y por tanto un método que no nos dará siempre un rendimiento correcto, y que siempre dependerá de que para que converja más a la solución correcta se deberán almacenar y utilizar cuantos más fotones mejor.
El método del mapeado de fotones es un método de dos pasos donde los pasos son:
1. Trazado Fotónico (Photon Tracing), construir el mapa de fotones trazando fotones desde las luces y a a través de la escena.
2. Radiación estimada (Radiance Estimate), estimar la radiación producida en un punto de la escena mediante estimación de densidad.
Así el mapa de fotones será construido usando 'Trazado fotónico' donde los fotones son emitidos desde las luces y almacenados al interactuar con las superficies del modelo. Una vez construido el mapa de fotones lo utilizaremos para calcular la luz radiada.

Transformaciones Geometricas
Las transformaciones geométricas son la o las operaciones geométricas que permiten crear una nueva figura a partir de una previamente dada. La nueva figura se llamará "homólogo" de la original.
Un sistema gráfico debería permitir la definición de objetos o imágenes que incluyan una serie de transformaciones. Estas son el medio para construir o modificar imágenes u objetos.
Las transformaciones se clasifican en:
· Directa: el homólogo conserva el sentido del original en el plano cartesiano
· Inversa: el sentido del homólogo y del original son contrarios
Además, también se pueden clasificar de acuerdo con la forma del homólogo con respecto al original en:
· Isométricas: el homólogo conserva las dimensiones y ángulos. También se llaman "movimientos", éstos son simetría axial y puntual, rotación y traslación.
· Isomórficas: el homólogo conserva la forma y los ángulos. existe proporcionalidad entre las dimensiones del homólogo con el original. una de ellas es la homotecia.
· Anamórficas: cambia la forma de la figura original. Una de ellas es la inversión (no la trataremos).
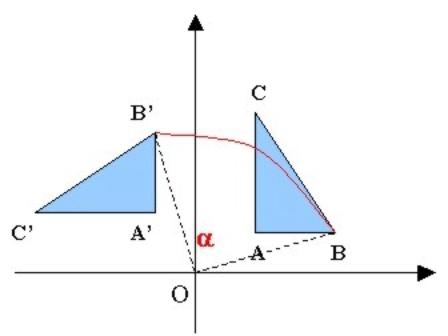
Las que trataremos son las de rotación, traslación y escalamiento. Cada transformación utiliza un punto (x,y) para generar un nuevo punto (x’,y’).
Los objetos se definen mediante un conjunto de puntos. Las transformaciones son procedimientos para calcular nuevas posiciones de estos puntos, cambiando el tamaño y orientación del objeto.
Un sistema gráfico debería permitir la definición de objetos o imágenes que incluyan una serie de transformaciones. Estas son el medio para construir o modificar imágenes u objetos.
Las transformaciones se clasifican en:
· Directa: el homólogo conserva el sentido del original en el plano cartesiano
· Inversa: el sentido del homólogo y del original son contrarios
Además, también se pueden clasificar de acuerdo con la forma del homólogo con respecto al original en:
· Isométricas: el homólogo conserva las dimensiones y ángulos. También se llaman "movimientos", éstos son simetría axial y puntual, rotación y traslación.
· Isomórficas: el homólogo conserva la forma y los ángulos. existe proporcionalidad entre las dimensiones del homólogo con el original. una de ellas es la homotecia.
· Anamórficas: cambia la forma de la figura original. Una de ellas es la inversión (no la trataremos).
Las que trataremos son las de rotación, traslación y escalamiento. Cada transformación utiliza un punto (x,y) para generar un nuevo punto (x’,y’).
Los objetos se definen mediante un conjunto de puntos. Las transformaciones son procedimientos para calcular nuevas posiciones de estos puntos, cambiando el tamaño y orientación del objeto.
Rotación: La rotación gira los puntos de una figura alrededor de un punto fijo. De la figura se obtiene:
x'=x*cos(a) - y*sen(a)
y=y*cos(a) - x*sen(a)
Translación: Consiste en mover los puntos de una figura desde una coordenada (x,y) hasta una (x’,y’) utilizando las siguientes fórmulas:
x’ = x + dx
y’ = y + dy
x’ = x + dx
y’ = y + dy
Escalamiento:El escalamiento modifica el tamaño de un polígono. Para obtener este efecto, se multiplica cada par coordenado (x,y) por un favor de escala en la dirección x y en la dirección y para obtener el par (x’, y’). Usamos las siguientes fórmulas:x’=x.Sxy’=y.Sy
Algoritmo Punto Medio de la Elipse
1. Se capturan el radio rx, ry y el centro de la circunferencia (xc,yc) y se obtiene el primer punto de una elipse
centrada en el origen como
(x0,y0) = (0,ry), donde 2 ry
2x = 0 y 2 rx2y = 2 rx2 ry
centrada en el origen como
(x0,y0) = (0,ry), donde 2 ry
2x = 0 y 2 rx2y = 2 rx2 ry
2. Se calcula el valor inicial del parámetro de decisión como
p10 = ry2 - rx2 ry + 1/4 rx2
3. En cada posición xk, en la región 1, iniciando en k=0, se efectúa la prueba siguiente:
Si p1k < 1 =" p1k" 1 =" p1k" 1 =" xk" 1 =" yk" p20 =" ry2(x0" k="0,"> 0, el siguiente punto a lo largo de la elipse centrada en (0,0) es
(xk,yk-1) y p2k+1 = p2k - 2 rx2yk+1 + rx2.
IV. ALGORITMO PUNTO MEDIO DE LA CIRCUNFERENCIA
Este algoritmo consiste en determinar el píxel más cercano a la circunferencia
• Consideremos el centro del círculo en (0,0)
• Comenzaremos en el punto (0,R) e iremos desde
x=0 hasta x=y, donde la pendiente va de 0 a -1
• Sólo pintaremos el primer octante
• Sea la función:
f(x,y) = x2 + y2 – R2
• Este test lo ejecutaremos en los puntos medios
entre los pixels que hay que decidir
<> (x,y) está dentro
= 0 -> (x,y) está sobre la circunferencia> 0 -> (x,y) está fuera

Supongamos ya dibujado el pixel (xk, yk)
pk = f (xk + 1, yk – ½) = (xk + 1)2 + (yk – ½)2 – R2
pk+1 = f (xk+1 + 1, yk+1 – ½) = (xk+1 + 1)2 + (yk+1 – ½)2 – R2
pk+1 = pk + 2xk+1 + 1 + (y2k+1–y2k) – (yk+1–yk)
0 ó 1 dependiendo del signo de pk
• Por lo tanto:
• Si pk <> pk+1 = pk + 2xk+1 + 1 -> hay que pintar el pixel (xk+1, yk)
• Si pk > 0 -> pk+1 = pk + 2xk+1 - 2yk+1 + 1 -> hay que pintar el pixel (xk+1, yk-1)
• Empezamos en el punto (0, R). ¿Cuánto vale p0?
p0 = f (1, R-1/2) =… = 5/4 – R -> no es entero!
Sin embargo, da igual. Podemos redondearlo, porque todos los incrementos son enteros,
y sólo queremos utilizar el signo de pk, y no su valor

• Consideremos el centro del círculo en (0,0)
• Comenzaremos en el punto (0,R) e iremos desde
x=0 hasta x=y, donde la pendiente va de 0 a -1
• Sólo pintaremos el primer octante
• Sea la función:
f(x,y) = x2 + y2 – R2
• Este test lo ejecutaremos en los puntos medios
entre los pixels que hay que decidir
<> (x,y) está dentro
= 0 -> (x,y) está sobre la circunferencia> 0 -> (x,y) está fuera

Supongamos ya dibujado el pixel (xk, yk)
pk = f (xk + 1, yk – ½) = (xk + 1)2 + (yk – ½)2 – R2
pk+1 = f (xk+1 + 1, yk+1 – ½) = (xk+1 + 1)2 + (yk+1 – ½)2 – R2
pk+1 = pk + 2xk+1 + 1 + (y2k+1–y2k) – (yk+1–yk)
0 ó 1 dependiendo del signo de pk
• Por lo tanto:
• Si pk <> pk+1 = pk + 2xk+1 + 1 -> hay que pintar el pixel (xk+1, yk)
• Si pk > 0 -> pk+1 = pk + 2xk+1 - 2yk+1 + 1 -> hay que pintar el pixel (xk+1, yk-1)
• Empezamos en el punto (0, R). ¿Cuánto vale p0?
p0 = f (1, R-1/2) =… = 5/4 – R -> no es entero!
Sin embargo, da igual. Podemos redondearlo, porque todos los incrementos son enteros,
y sólo queremos utilizar el signo de pk, y no su valor

Algoritmo de Bresenham
Considerado uno de los algoritmos más efectivos para el trazo de líneas mediante rastreo. Emplea cálculos incrementales con valores enteros. La forma de determinar el siguiente pixel a iluminar en la generación de una línea, se describe a continuación: Se parte de un punto inicial P1(Xinicial,Yinicial). Luego se desplaza una columna (incrementando la posición en X) y se traza el pixel cuyo valor de Y de la línea de rastreo se aproxima más a la trayectoria de la línea.
Se capturan los dos extremos de la línea P1(Xinicial,Yinicial) y P2(Xfinal,Yfinal), se ilumina el primer pixel correspondiente al extremo izquierdo de la línea(P1). Luego se calculan los parámetros que permitien decidir cuál será el proximo pixel a iluminar (DeltaX, DeltaY y ConstanteP). Dependiendo del valor que tome el Parámetro ConstanteP se evalúa y determina la coordenada a iluminar que puede ser: (X+1,Y) para ConstanteP < 0, en caso contrario se ilumina (X+1,Y+1). El proceso anterior debe repetirse 4DeltaX veces.
Leer Coordenadas P1(Xinicial, Yinicial)
Leer Coordenadas P2(Xfinal, Yfinal)
Asignar a DeltaX el ABS( Xfinal - Xinicial)
Asignar a DeltaY el ABS( Yfinal -Yinicial)
Asignar a ConstanteP el resultado de 2*DeltaY - DeltaX
Si Xinicial > Xfinal
Asignar Xfinal a X
Asignar Yfinal a Y
Asignar Xinicial a Ultimo
De lo contrario
Asignar Xinicial a X
Asignar Yinicial a Y
Asignar a Xfinal a Ultimo
Iluminar pixel en coordenada X,Y
Hacer mientras X sea menor que elUltimo
Asignar X + 1 a X
Si ConstanteP < 0
Asignar ConstanteP + 2 *DeltaY a ConstanteP
De lo contrario
Asignar Y+1 a Y
Asignar a ConstanteP el resultado de ConstanteP+2 *(DeltaY-DeltaX)
Iluminar pixel en coordenada X,Y
Fin de Algoritmo (Bresenham)

Se capturan los dos extremos de la línea P1(Xinicial,Yinicial) y P2(Xfinal,Yfinal), se ilumina el primer pixel correspondiente al extremo izquierdo de la línea(P1). Luego se calculan los parámetros que permitien decidir cuál será el proximo pixel a iluminar (DeltaX, DeltaY y ConstanteP). Dependiendo del valor que tome el Parámetro ConstanteP se evalúa y determina la coordenada a iluminar que puede ser: (X+1,Y) para ConstanteP < 0, en caso contrario se ilumina (X+1,Y+1). El proceso anterior debe repetirse 4DeltaX veces.
Leer Coordenadas P1(Xinicial, Yinicial)
Leer Coordenadas P2(Xfinal, Yfinal)
Asignar a DeltaX el ABS( Xfinal - Xinicial)
Asignar a DeltaY el ABS( Yfinal -Yinicial)
Asignar a ConstanteP el resultado de 2*DeltaY - DeltaX
Si Xinicial > Xfinal
Asignar Xfinal a X
Asignar Yfinal a Y
Asignar Xinicial a Ultimo
De lo contrario
Asignar Xinicial a X
Asignar Yinicial a Y
Asignar a Xfinal a Ultimo
Iluminar pixel en coordenada X,Y
Hacer mientras X sea menor que elUltimo
Asignar X + 1 a X
Si ConstanteP < 0
Asignar ConstanteP + 2 *DeltaY a ConstanteP
De lo contrario
Asignar Y+1 a Y
Asignar a ConstanteP el resultado de ConstanteP+2 *(DeltaY-DeltaX)
Iluminar pixel en coordenada X,Y
Fin de Algoritmo (Bresenham)

Algoritmo DDA
DDA= Digital Differential Analyzer
DeltaX = DeltaY / m DeltaY = m * DeltaX
Es un algoritmo que se basa en el cálculo y la evaluación de un DeltaX ( X) y un DeltaY( Y). Por medio de las siguientes ecuaciones:
Se efectúa un muestreo de la línea en intervalos unitarios en una coordenada y se determinan los valores enteros correspondientes más próximos a la trayectoria de la línea para la siguiente coordenada.
Se aceptan como datos de entradas las dos posiciones de los pixeles correspondientes a los extremos de la línea P1(Xinicial,Yinicial) y P2(Xfinal,Yfinal). Las diferencias horizontal y vertical entre las posiciones de los extremos dados, se asignan a las variables DeltaX y DeltaY respectivamente. La diferencia con la mayor magnitud determina el valor del parámetro Pasos. Se procede a determinar la compensación necesaria (incremento), para generar la posición del pixel siguiente a lo largo de la trayectoria de la línea. Luego, se ilumina la posición en la pantalla y se repite este proceso cíclico Pasos Veces, hasta obtener la línea deseada.
Algoritmo:
Leer Coordenadas P1(Xinicial, Yinicial)
Leer Coordenadas P2(Xfinal,Yfinal)
Asignar a DeltaX la diferencia de Xfinal - Xinicial
Asignar a DeltaY la diferencia de Yfinal - Yinicial
Si ABS( DeltaX) > ABS(DeltaY)
Asignar a Pasos el ABS(DeltaX)
De lo contrario
Asignar a Pasos el ABS(DeltaY)
Asignar a Xincremento el resultado de DeltaX / Pasos
Asignar a Yincremento el resultado de DeltaY / Pasos
Asignar a X el valor de Xinicial
Asignar a Y el valor de Yinicial
Iluminar pixel en coordenada X,Y
Desde k=1 hasta Pasos
Asignar a X la suma de X + Xincremento
Asignar a Y la suma de Y + Yincremento
Iluminar pixel en Coodenada X,Y
Fin de Algoritmo(DDA)
Se efectúa un muestreo de la línea en intervalos unitarios en una coordenada y se determinan los valores enteros correspondientes más próximos a la trayectoria de la línea para la siguiente coordenada.
Se aceptan como datos de entradas las dos posiciones de los pixeles correspondientes a los extremos de la línea P1(Xinicial,Yinicial) y P2(Xfinal,Yfinal). Las diferencias horizontal y vertical entre las posiciones de los extremos dados, se asignan a las variables DeltaX y DeltaY respectivamente. La diferencia con la mayor magnitud determina el valor del parámetro Pasos. Se procede a determinar la compensación necesaria (incremento), para generar la posición del pixel siguiente a lo largo de la trayectoria de la línea. Luego, se ilumina la posición en la pantalla y se repite este proceso cíclico Pasos Veces, hasta obtener la línea deseada.
Algoritmo:
Leer Coordenadas P1(Xinicial, Yinicial)
Leer Coordenadas P2(Xfinal,Yfinal)
Asignar a DeltaX la diferencia de Xfinal - Xinicial
Asignar a DeltaY la diferencia de Yfinal - Yinicial
Si ABS( DeltaX) > ABS(DeltaY)
Asignar a Pasos el ABS(DeltaX)
De lo contrario
Asignar a Pasos el ABS(DeltaY)
Asignar a Xincremento el resultado de DeltaX / Pasos
Asignar a Yincremento el resultado de DeltaY / Pasos
Asignar a X el valor de Xinicial
Asignar a Y el valor de Yinicial
Iluminar pixel en coordenada X,Y
Desde k=1 hasta Pasos
Asignar a X la suma de X + Xincremento
Asignar a Y la suma de Y + Yincremento
Iluminar pixel en Coodenada X,Y
Fin de Algoritmo(DDA)
Suscribirse a:
Entradas (Atom)