Transformaciones Geometricas

Las transformaciones geométricas son la o las operaciones geométricas que permiten crear una nueva figura a partir de una previamente dada. La nueva figura se llamará "homólogo" de la original.
Un sistema gráfico debería permitir la definición de objetos o imágenes que incluyan una serie de transformaciones. Estas son el medio para construir o modificar imágenes u objetos.
Las transformaciones se clasifican en:
· Directa: el homólogo conserva el sentido del original en el plano cartesiano
· Inversa: el sentido del homólogo y del original son contrarios
Además, también se pueden clasificar de acuerdo con la forma del homólogo con respecto al original en:
· Isométricas: el homólogo conserva las dimensiones y ángulos. También se llaman "movimientos", éstos son simetría axial y puntual, rotación y traslación.
· Isomórficas: el homólogo conserva la forma y los ángulos. existe proporcionalidad entre las dimensiones del homólogo con el original. una de ellas es la homotecia.
· Anamórficas: cambia la forma de la figura original. Una de ellas es la inversión (no la trataremos).
Las que trataremos son las de rotación, traslación y escalamiento. Cada transformación utiliza un punto (x,y) para generar un nuevo punto (x’,y’).
Los objetos se definen mediante un conjunto de puntos. Las transformaciones son procedimientos para calcular nuevas posiciones de estos puntos, cambiando el tamaño y orientación del objeto.

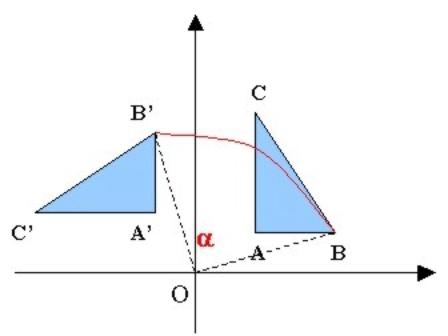
Rotación: La rotación gira los puntos de una figura alrededor de un punto fijo. De la figura se obtiene:

x'=x*cos(a) - y*sen(a)

y=y*cos(a) - x*sen(a)

Translación: Consiste en mover los puntos de una figura desde una coordenada (x,y) hasta una (x’,y’) utilizando las siguientes fórmulas:
x’ = x + dx
y’ = y + dy

Escalamiento:El escalamiento modifica el tamaño de un polígono. Para obtener este efecto, se multiplica cada par coordenado (x,y) por un favor de escala en la dirección x y en la dirección y para obtener el par (x’, y’). Usamos las siguientes fórmulas:x’=x.Sxy’=y.Sy